The Monad in Pythagorean Thought
Pythagorean Monad, a foundational principle that represents absolute unity and serves as the origin of all
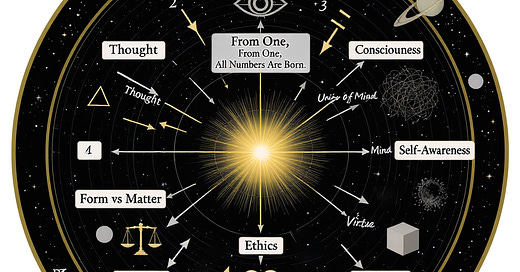
At the heart of Pythagorean philosophy lies the concept of the monad, a foundational principle that represents absolute unity and serves as the origin of all. Unlike other numbers that can be divided or combined, the monad remains singular and indivisible—a quality that the Pythagoreans regarded as inherently divine. In their view, this singularity was not merely a mathematical abstraction but a metaphysical reality, embodying the purest form of being from which all multiplicity arises. The monad was seen as the first cause, the primordial source from which all subsequent numbers, forms, and structures emerge. This understanding positioned it at the center of Pythagorean cosmology, where it functioned as both the starting point of creation and the ultimate goal toward which all things return.
Represented by a simple point in geometry, it was considered the most fundamental shape—possessing position but no dimension, existing without extension yet serving as the basis for all measurable forms. This paradoxical nature fascinated the Pythagoreans, who saw in it a reflection of the ineffable nature of the divine. Just as a geometric point has no length, width, or depth yet defines space itself, so too does the monad transcend material limitations while simultaneously giving rise to all structured reality. The Pythagoreans believed that numbers were not merely quantitative tools but living principles that governed the cosmos, and the monad stood at the apex of this numerical hierarchy as the ultimate generative force.
The monad’s importance extended beyond arithmetic and geometry into the realm of metaphysics, where it symbolized the essence of identity and selfhood. The Pythagoreans recognized that for any entity to exist as itself, it must possess a principle of sameness—an unchanging core that distinguishes it from all else. This fundamental attribute of individuality was traced back to the monad, which provided the conceptual foundation for logic, knowledge, and rational thought. Without the monadic principle of unity, differentiation would be impossible; nothing could maintain a consistent nature, and reality itself would dissolve into chaos. Thus, the monad was not only the source of numbers but also the very condition that made coherent possible.
The Generative Power of the Monad
The Pythagoreans viewed the monad not merely as a static point of unity but as the dynamic source from which all multiplicity originates. In their numerical system, every number proceeds from the monad, making it the foundational element of all mathematical relationships. This generative capacity was central to their understanding of reality, as they believed that numbers were not just abstract symbols but active principles shaping the structure of the cosmos. The sequence of numbers, beginning with one, unfolds naturally through addition: 1 generates 2, 2 generates 3, and so forth, illustrating how complexity arises from simplicity. This process mirrored the Pythagorean conception of creation itself, wherein the universe emerges from the singular divine source represented by the monad. Just as numbers derive their meaning and order from the initial unit, so too do all beings and phenomena trace their existence back to this primal unity.
This perspective led the Pythagoreans to see the monad as more than a mere numerical starting point—it was the very engine of cosmic generation. They understood the unfolding of numbers as a reflection of the broader movement from unity to diversity, a principle that governed not only mathematics but also nature and metaphysics. The monad contained within itself the potential for all subsequent numbers, much like a seed contains the blueprint for an entire tree. Though seemingly simple, the monad was not empty or inert; rather, it was a concentrated fullness, a source of infinite possibility. From this singular point, the entire spectrum of numerical relationships emerged, forming the basis for proportion, harmony, and structure throughout the universe. The Pythagoreans saw in this progression a model for how order arises from chaos, how form emerges from formlessness, and how the cosmos itself is structured upon the interplay between unity and multiplicity.
The monad's role as the generator of numbers had profound implications for the Pythagorean understanding of reality. They believed that the cosmos was fundamentally mathematical, constructed according to precise numerical ratios and harmonic principles. Since all numbers derived from the monad, it followed that all aspects of existence—whether physical, ethical, or aesthetic—were ultimately expressions of this primary unity. This belief influenced their approach to music, astronomy, and even ethics, where they sought to uncover the underlying numerical patterns that governed beauty, justice, and the movements of celestial bodies. By tracing these patterns back to their source in the monad, the Pythagoreans found a unifying principle that connected disparate domains of knowledge, reinforcing their conviction that the universe was an ordered whole emanating from a single divine origin.
Beyond its role as the generative source of numbers, the monad embodied the principle of wholeness and completeness, representing the idea that true unity is not merely the absence of division but the presence of an integrated totality. For the Pythagoreans, the number one was not simply the first in a sequence but the embodiment of self-sufficiency and integrity. It signified a state in which nothing is lacking, a perfect equilibrium where all potentialities coexist in harmonious balance. This notion of completeness extended beyond the mathematical realm, influencing the Pythagorean understanding of identity, consciousness, and the structure of reality itself. The monad was seen as the essential nature of any entity, the irreducible core that gives something its distinct being. Without this principle of unity, existence would lack coherence, and individual entities could not maintain their identities amidst the flux of change.
This understanding of the monad as the foundation of identity was closely linked to the Pythagorean concept of self-identity, a principle that underpins all logical reasoning and cognitive recognition. The Pythagoreans recognized that for anything to be known or differentiated, it must possess a stable, self-contained nature that allows it to be consistently identified across time and experience. This principle of sameness, which enables an object to remain itself despite transformations, was traced back to the monad as its ultimate source. Just as a geometric point maintains its position regardless of its relationship to other points, so too does the monad serve as the fixed reference point around which all distinctions and relations are organized. Without this anchoring principle of unity, the world would dissolve into an indistinguishable blur, devoid of recognizable forms or meaningful differences. The Pythagoreans saw this as a fundamental truth about reality—that the ability to perceive and understand the world depends on the presence of an underlying unity that stabilizes and orders experience.
The monad’s role as the principle of identity had profound implications for the Pythagorean worldview, shaping their approach to knowledge, ethics, and metaphysics. If all things derive from the monad, then beneath the surface of apparent diversity, there exists a deeper unity that connects all beings. This insight led the Pythagoreans to seek hidden harmonies and correspondences among different aspects of reality, believing that by understanding the numerical relationships that govern existence, they could uncover the fundamental unity that binds all things together. Their pursuit of mathematical knowledge was thus not merely an intellectual exercise but a philosophical quest to reveal the underlying structure of reality, a structure that ultimately pointed back to the monad as its source and foundation.
The Monad as a Dynamic Principle of Multiplicity
Though the monad is defined by its absolute simplicity, the Pythagoreans did not regard it as a static or passive entity; rather, they saw it as a dynamic principle capable of generating all subsequent complexity. This paradox—that absolute simplicity could give rise to boundless multiplicity—was central to their philosophical framework. The monad, in its undivided unity, contained within itself the potential for all numerical expansion, acting as both the origin and the sustaining force behind the emergence of diverse forms. Unlike composite entities that require external elements to achieve complexity, the monad was understood to possess an inherent richness, a fullness that was not diminished by division but instead revealed greater depths through the unfolding of multiplicity. This generative capacity was not merely a mechanical process of enumeration but a profound metaphysical principle, reflecting the way in which the cosmos itself unfolds from a singular divine source.
The Pythagoreans drew an analogy between the monad’s creative power and the principles of music and harmony. Just as a single note can give rise to an entire scale through the application of mathematical ratios, so too does the monad serve as the fundamental tone from which all numerical relationships arise. In this sense, the monad was not simply the first number but the key to understanding the proportional structures that define beauty, order, and intelligibility in the universe. The Pythagoreans observed that musical intervals such as the octave, fifth, and fourth could be expressed through simple numerical ratios (2:1, 3:2, 4:3), demonstrating that harmony itself was rooted in numerical relationships. These relationships, in turn, traced their lineage back to the monad, reinforcing the idea that the same principle governing musical consonance also underpinned the structure of reality itself.
This understanding of the monad as a dynamic generator of multiplicity had profound implications for the Pythagorean conception of the cosmos. They believed that the universe was not a chaotic aggregation of random elements but a carefully structured system governed by mathematical laws. The monad, as the source of all numbers, was thus the ultimate architect of this order, ensuring that complexity emerged in accordance with rational principles. This perspective informed their studies in astronomy, where they sought to uncover the numerical patterns that governed planetary motion, and in ethics, where they explored how mathematical proportion could guide virtuous behavior. The monad’s generative power was not confined to abstract theory; it was a living force that shaped the fabric of existence, revealing itself in the intricate patterns of nature, art, and human thought.